The "Russian Roulette" sampling technique (which is creepily named, but is known officially as so) is a sampling technique used in ray tracing to reduce the number of samples for evaluating some value, while maintaining the convergence. It was very mystifying at first sight, but became very intuitive when I came up of a graphical explanation.
Shortly put, the Russian Roulette sampling technique can be interpreted as making "copies" of high-order terms, to use in place of the dropped off terms that were not evaluated in other samples. This can be described graphically using the following figure.
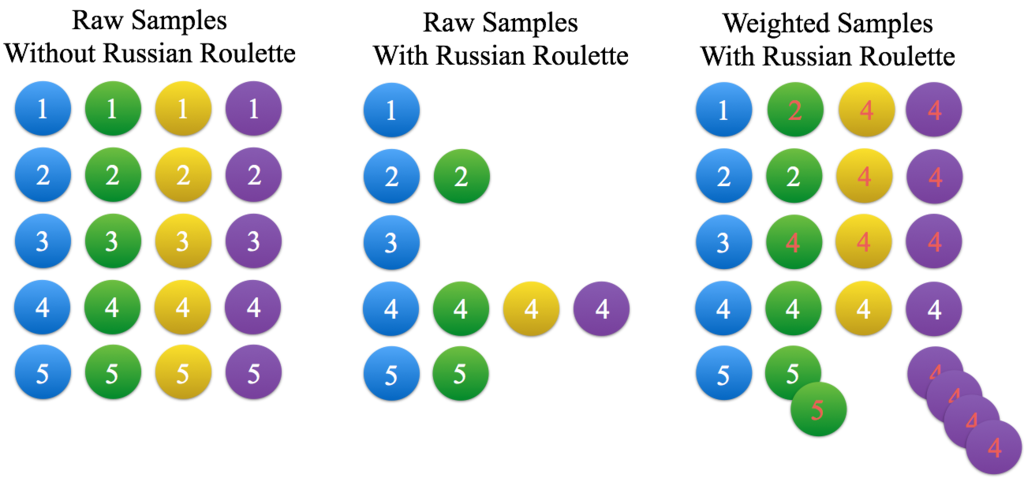
Let us consider a problem where we want to evaluate 4 orders of some value, with 5 samples. In ray tracing, this could be evaluating the radiance using terms of up to 4 reflections with 5 samples, for instance. In the figure above, the colors correspond to the orders of the value, and the number n in the circle indicates that it is the n-th sample.
The leftmost figure shows a direct method of evaluating this value, that is to just simply evaluate all of the orders in all of the samples. However, in ray tracing it can be time-consuming to do such evaluations.
This is where the Russian Roulette sampling technique comes in. In the Russian Roulette technique, we aim to evaluate only a few high-order terms. Basically, before evaluating each order of terms, we roll some dice - and proceed to evaluate high order terms at only a given probability, or else halt the evaluation and move on to the next samples. Each higher order term must survive this judgement before it gets evaluated, or otherwise the "game" (higher-term evaluation) ends and moves on to the next round (sample) - therefore, the name "Russian Roulette." In this figure, we've assumed a 50% probability of proceeding to evaluate the next higher order. The figure on the center shows the actually calculated terms in each sample, for the Russian Roulette. In other words, the circles in the figure are the circles that "survived" the Roulette. Notice that the number of evaluations is reduced to around half of that in the left figure, and many high orders are dropped off.
Now, since we have excluded many orders, we don't have enough circles (terms) to add up to calculate the average. (i.e., simply taking the average of all of the terms (circles) provides an inaccurate estimate of the true value, compared to the estimator shown on the left figure.) Specifically, each n-th order term shows up at a ratio of (1/2)^(n-1) compared to the number of them in the left figure.
How do we calculate the average with such few circles (terms)? The answer, which is the Russian Roulette sampling technique, is to use copies of other circles (terms) as placeholders. Mathematically, the technique is to divide the value of each evaluated term by the probability of its appearance when taking the grand average. This obscure technique can be understood by observing the right side of the figure. Dividing the term by its survival probability p is equivalent to considering as if 1/p copies of that term has existed in the evaluation. This is the whole idea of the sampling technique, and is depicted in the figure above as copies of the circle. (Copies are indicated by red index numbers.) By making "copies" in such a way, the number of samples of each order approximately match that of the direct technique shown in the left side of the first figure. Although the number of circles differ from its true value (they are short in the 3rd order and excessive in the 2nd and 4th order), if we take a sufficient number of samples, the law of large numbers helps us to diminish those discrepancies to an ignorable level. Therefore, the "magic" of dividing higher order terms in the Russian Roulette technique, can be interpreted as making the "right number of copies" of that term, so that it properly compensates for the higher order terms that did not survive to be evaluated (i.e. dropped in the sampling process).
