Survey: Marschner, et al. (2003), Light scattering from human hair fibers (The Marschner Model)

As I had an opportunity to read and implement Marschner's paper [1] on the Marschner Model, I would like to share the details and points I have stumbled upon on reading the paper. The Marschner Model is a model proposed in 2003, that describes how light is scattered (reflected and transmitted) in human hair. It is used to implement shaders for human hair models, and rendering realistic hair.
[1] MARSCHNER, S. R., et al., 2003. Light scattering from human hair fibers. ACM Trans. Graph. 22, 3, 780–791. http://www.graphics.stanford.edu/papers/hair/

For conducting this survey, I've also referenced the following blog post:
Marschner Shader Part II | Real-Time Hair Simulation and Rendering

Overview

The Marschner Model is essentially a scattering function ${S(\omega_i,\omega_r)}$ , which lets you find how much light is redirected from one direction to another. Simply put, it is the ratio of incoming light intensity from direction ${\omega_i}$ against the outcoming light intensity from direction ${\omega_r}$ . Given an outcoming direction ${\omega_r}$ , it can be used as

${ \bar L_r(\omega_r) = D \int S(\omega_i, \omega_r) L_i(\omega_i) \cos \theta_i\, d \omega_i, }$

to determine the amount of light emitted in that direction.

Here, ${\bar L}$ is the intensity per *length* (which is different from ordinary *radiance*, which is intensity per *area*), which they call as *curve intensity*.

${D}$ is the diameter of the hair - which implies that outcoming light increases for thicker hair, i.e. thicker hairs are more shiny.

One novel point of the Marschner Model is that ${S}$ is a function of only the *direction* of incidence, and not the *position* of incidence, meaning that the hair's thickness is *taken out of thought*. In the derivation, the hair's thickness (the position of ray-hair intersection) is explicitly considered, but is effectively ignored in its final form.

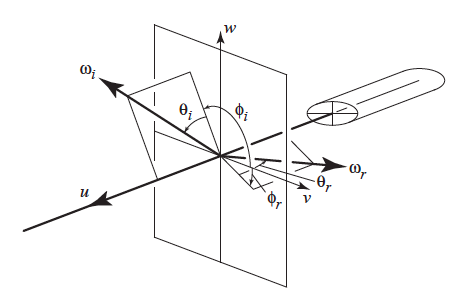
Figure 1. The coordinate system. Image cited from Marschner, et al. (2003) [1]

One important point that I've stumbled upon is the coordinate system. Although at first sight it seems like an ordinary spherical system with ${w}$ as the ${z}$ direction, that is actually not the case. Here, ${\theta_i}$ and ${\theta_r}$ are measured as the inclination to the ${w}$ - ${v}$ plane. Therefore,

${ \begin{align} \theta_i &:= \frac \pi 2 - \cos^{-1} (\omega_i \cdot u), \\ \phi_i &:= \tan^{-1} \left(\frac{\omega_i \cdot w}{\omega_i \cdot v}\right). \\ \end{align} }$
The same holds for ${\omega_r}$ .

In the paper, the hair is modeled as an elliptic cylinder with a bumpy surface (which models cuticles). They first start with an ideal, smooth cylinder case, where ${S}$ is given as

${ S(\phi_i, \theta_i ; \phi_r, \theta_r) = \delta(\theta_r + \theta_i) N(\eta'(\theta); \phi_i, \phi_r) / \cos^2 \theta. }$

Where ${\delta}$ is the delta function.
The term ${\delta(\theta_r + \theta_i)}$ implies that scattering only occurs when ${\theta_r = \theta_i}$ , which ultimately implies that an incoming straight ray is emitted in the shape of a cone.

We can see that ${S}$ is decomposed into ${\theta}$ -dependent parts and ${\phi}$ -dependent parts. This is one of the important features of this model, derived from the symmetry of the cylindric geometry of the hair.

The actual Marschner Model is an extention of this equation,

${ \begin{align} S(\phi_i, \theta_i ; \phi_r, \theta_r) &=M_{R} (\theta_h) N_{R} (\eta'(\eta,\theta_d); \phi) / \cos^2 \theta_d \\ &+M_{TT} (\theta_h) N_{TT} (\eta'(\eta,\theta_d); \phi) / \cos^2 \theta_d \\ &+M_{TRT}(\theta_h) N_{TRT}(\eta'(\eta^*(\phi_h),\theta_d); \phi) / \cos^2 \theta_d. \end{align} }$

Although there are more terms, all emitted light is still contained in a single cone. The 3 terms represent the 3 modes of scattering that are considered (all modes are in the same cone). We can recognize that one major extension is the replacement of ${\delta(\theta_r + \theta_i)}$ with ${M(\theta_h)}$ .

${\eta '}$ is one of the difficult parts of this paper. In this paper, simply put, *3D Fresnel effects are evaluated as 2D Fresnel effects with an augmented index of refraction,* thanks to the symmetry of hair (c.f. p. 6). We know that in Fresnel reflections/refractions, all light paths are contained in one plane. Obviously, this plane does not necessarily run parallel to the surface normal of the hair, and can be tilted (i.e., the plane may not cross the hair orthogonally). In this paper, the "3D" light path (on the tilted plane) is projected on to the plane perpendicular to the hair surface. Then, the Fresnel equations are evaluated *on the projected plane*, and then *projected back to the original tilted plane*. The augmented index of refraction, used on the projected plane, is ${\eta '}$ - which only depends on ${\theta}$ due to the projection.

The Model

${M}$ is a "unit-integral, zero-mean lobe function with width ${\beta}$ " (c.f. p.8), i.e. simply a probability distribution ${g}$ :

${ \begin{align} M_{R} (\theta_h) &= g(\alpha_{R} , \beta_{R} ;\theta_h) \\ M_{TT} (\theta_h) &= g(\alpha_{TT} , \beta_{TT} ;\theta_h) \\ M_{TRT}(\theta_h) &= g(\alpha_{TRT}, \beta_{TRT};\theta_h) \end{align} }$

In the paper, ${g(\alpha, \beta, x)}$ is given as a normalized Gaussian function with mean ${\alpha}$ and standard deviation ${\beta}$ :
${ g(\alpha, \beta, x) = \frac 1 {\sqrt{2 \pi \beta^{2}}} \exp \left(-\frac{(x - \alpha)^2}{2\beta^{2}} \right). }$

The notation for the dependency of ${\alpha}$ on ${g}$ is changed for clarity.

${N}$ is complicated to find. First, as a notation, the paths ${R, TT, TRT}$ are given an index ${p=0,1,2}$ , respectively. Then:

${ \begin{align} N_p(\eta'(\eta,\theta_d),p,\phi) &:= \sum_{\gamma_i \in \Gamma} A(p,h(p,\gamma_i,\phi)) \left| 2 \frac {d\hat\phi} {dh}(p, h(p,\gamma_i,\phi)) \right|^{-1}. \end{align} }$
Here, ${\phi := \phi_i - \phi_t}$ . This means that ${N_p}$ depends on the azimuths through only their *difference*.

We have additionally written the ${\eta'(\eta,\theta_d)}$ -dependency of ${N_p}$ and ${h}$ .
The notation of the sum and the arguments of ${h}$ were changed for clarity.
Confusingly, in the original paper there is a *variable* ${\phi := \phi_i - \phi_t/2}$ and a *function* ${\phi(p,\gamma_i)}$ which are different quantities. ${\phi(p,\gamma_i)}$ is a trigonometric function (c.f. p.6) and is later approximated as ${\hat \phi(p,\gamma_i)}$ (c.f. p.8). For brevity, we will write ${\hat \phi}$ in place of the original function ${\phi(p,\gamma_i)}$ .

Below, we will study the actual forms of each term.

Definition of ${\eta'}$ , ${\eta''}$ :

${\eta'}$ , ${\eta''}$ are the corrected values of ${\eta}$ :

${ \begin{align} \eta'(\eta, \varphi) &:= \sqrt{\eta^2 - \sin^2 \varphi} \Big/ \cos \varphi\\ \eta''(\eta, \varphi) &:= \eta^2 \cos \varphi \Big/ \sqrt{\eta^2 - \sin ^2 \varphi} \end{align} }$

Here, ${\eta}$ is a constant (c.f. p.8).

Definition of ${F}$ :

${F}$ is the corrected Fresnel reflectance function, computed with the corrected refraction indices ${\eta', \eta''}$ .

We know the ordinary Fresnel reflectance functions are given as:

${ \begin{align} F_s(\eta_1, \eta_2, \varphi) &:= \frac {\eta_1 \cos \varphi - \eta_2 \cos \varphi'} {\eta_1 \cos \varphi + \eta_2 \cos \varphi'} \\ F_t(\eta_1, \eta_2, \varphi) &:= \frac {\eta_1 \cos \varphi' - \eta_2 \cos \varphi} {\eta_1 \cos \varphi' + \eta_2 \cos \varphi} \\ \varphi' &:= \sin^{-1}\left(\frac{\eta_1}{\eta_2}\sin \varphi \right) \end{align} }$

The corrected Fresnel function ${F}$ is then defined as
${ \begin{align} F(\eta', \eta'', \varphi) &:= \frac {F_s(1,\eta'(\varphi),\varphi)^2 + F_t(1,\eta''(\varphi),\varphi)^2} 2. \end{align} }$

c.f. p.12:

...factor for oblique incidence may be computed from the projected angles by using ${\eta'}$ for the perpendicular component of the reflectance and a second index, ${\eta''}$ .

Finding ${\gamma_i}$ and ${h, \gamma_t}$ :

${\gamma_i}$ is found by solving a cubic equation. First define

${ \begin{align} \theta_d &:= \frac{(\theta_r - \theta_i)} 2 \\ \eta' &:= \eta'(\eta,\theta_d) \\ c &:= \sin^{-1}(1/\eta') \\ % \phi(p,h) &:= 2p\gamma_t - 2\gamma_i + p\pi \\ \hat \phi(p,\gamma_i) &:= \left( \frac{6pc} \pi - 2 \right) \gamma_i - \frac{8pc}{\pi^3} \gamma_i^3 + p \pi \end{align} }$

${\gamma_i}$ is then the solution of the equation

${ \hat \phi(p,\gamma_i) - \phi = 0. }$

Let ${\gamma_i \in \Gamma}$ be all of the solutions of ${\gamma_i}$ . (Recall that ${\Gamma}$ is a symbol newly defined in this blog post.)

It is mentioned (c.f. p.6) that for ${p \geq 2}$ , there may be one or three solutions to this equation, i.e. for the path ${TRT}$ there may be multiple incident directions that end up being emitted in a specific direction.

For each solution of ${\gamma_i}$ , we finally calculate ${h}$ and ${\gamma_t}$ :

${ \begin{align} h &:= h(p, \gamma_i, \phi) := \sin \gamma_i \\ \gamma_t &:= \sin^{-1}\frac h {\eta'} \\ \end{align} }$

Finding ${A}$ :

${A}$ is the attenuation factor:

${ \begin{align} T(\sigma_a, h) &:= \exp\left(-\sigma_a(2 + 2\cos 2\gamma_t) \right) \\ \sigma'_a &:= \sigma_a/\cos \theta_t \\ A(p,h) &:= \begin{cases} F(\eta',\eta'',\gamma_i) & p = 0 \\ \left(1 - F(\eta',\eta'',\gamma_i) \right)^2 F\left( \frac 1 {\eta'}, \frac 1 {\eta''}, \gamma_t \right)^{p-1} T(\sigma'_a,h)^p & p > 0 \\ \end{cases} \end{align} }$
Where ${\theta_t}$ is the "inclination to the axis" (c.f. p.7). Although this symbol is newly defined here in this sentence, we can infer that ${\theta_t = \theta_d}$ , since ${\theta_d}$ is the inclination used to determine the effective index of refraction ${\eta'}$ .

Finding ${d\hat\phi/dh}$ :

Using the approximation,

${ \begin{align} \frac{d\hat\phi}{dh} &= \frac{d\hat\phi}{d\gamma_i} \frac{d\gamma_i}{dh} \\ &= \frac {\left( \frac{6pc} \pi - 2 \right) - \frac{24pc}{\pi^3} \gamma_i^2} {\sqrt{1 - h^2}}. \end{align} }$

Finding ${N_p}$ :

Let us finally recall the form of ${N_p}$ :

${ \begin{align} N_p(p,\phi) &:= \sum_{\gamma_i \in \Gamma} A(p,h(p,\gamma_i,\phi)) \left| 2 \frac {d\hat\phi} {dh}(p, h(p,\gamma_i,\phi)) \right|^{-1}. \end{align} }$
One important fact is that the sum on the right hand side is taken over all solutions ${\gamma_i \in \Gamma}$ , i.e. for all paths corresponding to the azimuth ${\phi}$ .

The Grand Result

If we shall write the explicit form of one mode ${M_pN_p}$ for the sake of reference (which becomes quite messy),

${ \begin{align} &M_p (\theta_h) N_p(\eta'(\eta,\theta_d),p,\phi) \\ =& \frac 1 {\sqrt{2 \pi \beta_p^{2}}} \exp \left(-\frac{(x - \alpha_p)^{2}}{2\beta_p^{2}} \right) \times \\ &\sum_{\gamma_i \in \Gamma} \left[ %A(p,h(p,\gamma_i,\phi)) \left( \begin{cases} F(\eta',\eta'',\gamma_i) & p = 0 \\ \left(1 - F(\eta',\eta'',\gamma_i) \right)^{2} F\left( \frac 1 {\eta'}, \frac 1 {\eta''}, \gamma_t \right)^{p-1} T(\sigma'_a,h)^p & p > 0 \\ \end{cases} \right) \times \right.\\ & \left.\left| 2 \frac {\left( \frac{6pc} \pi - 2 \right) - \frac{24pc}{\pi^3} \gamma_i^{2}} {\sqrt{1 - h^{2}}} \right|^{-1}\right], \end{align} }$

where ${\gamma_i \in \Gamma}$ are defined by the solutions for the cubic equation
${ \left( \frac{6pc} \pi - 2 \right) \gamma_i - \frac{8pc}{\pi^3} \gamma_i^3 + p \pi - \phi = 0. }$
${S(\omega_i, \omega_r)}$ is then a sum of the modes over the paths ${p \in \{0,1,2\}}$ :
${ S(\omega_i, \omega_r) = \sum_p M_pN_p. }$

Overview

The Model

Definition of , :

Definition of :

Finding and :

Finding :

Finding :

Finding :

The Grand Result

Definition of ${\eta'}$ , ${\eta''}$ :

Definition of ${F}$ :

Finding ${\gamma_i}$ and ${h, \gamma_t}$ :

Finding ${A}$ :

Finding ${d\hat\phi/dh}$ :

Finding ${N_p}$ :